L’objectif est de recréer à une distance non limitée l’état quantique d’une particule, par exemple le spin d’un electron.L’electron lui même n’est pas "téléporté" mais son état de spin, recréé sur un autre electron rend ce nouvel electron indistinguable de l’electron d’origine.
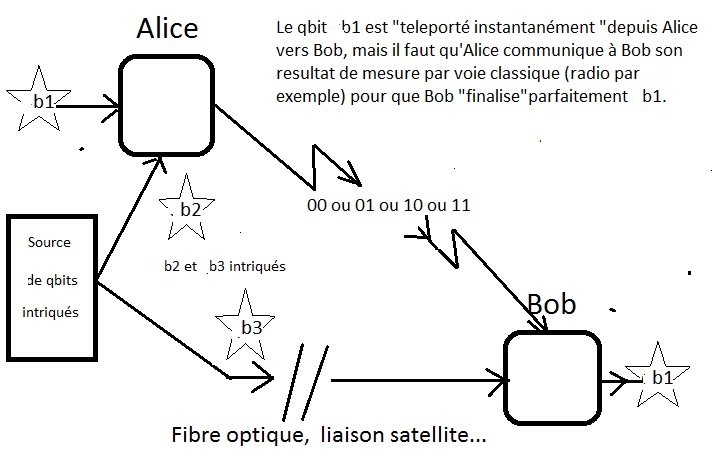
L’état de l’electron est encodé dans le qbit b1(quantum bit, pour un rappel des definitions et les différentes portes quantiques, voir l’Annexe).
Une source génère un couple de qbits intriqués, b2 et b3.
Alice et Bob récupèrent chacun leur qbit.
On notera que Bob peut être éloigné d’Alice de plusieurs milliers de kilomètres ( une experience d’intrication par liaison satellite a été réalisée avec succès durant l’été 2017 ).
 Alice
intrique b1 et son qbit b2.
Alice
intrique b1 et son qbit b2.
b2 et b3 étant déjà intriqués, ceci revient à intriquer indirectement b1 avec b3
 Alice
effectue ensuite une mesure partielle (mesure de Bell) sur l’état
obtenu.
Alice
effectue ensuite une mesure partielle (mesure de Bell) sur l’état
obtenu.
Cette mesure fournit l’une des 4 valeurs : 00, 01, 10 ou 11 et laisse b3 dans un état résiduel proche de l’état b1, et ce instantanément.
 Alice
communique à Bob la valeur obtenue par un canal habituel ( vitesse
inférieure à la lumière)
Alice
communique à Bob la valeur obtenue par un canal habituel ( vitesse
inférieure à la lumière)
 Bob,
en fonction de cette valeur applique (ou non) un traitement local à son
qbit b3
Bob,
en fonction de cette valeur applique (ou non) un traitement local à son
qbit b3
 Le
qbit b3 est alors identique à b1
Le
qbit b3 est alors identique à b1
On note que b1 détruit dans l’opération n’a donc pas été cloné, le clonage de qbit étant interdit en théorie quantique
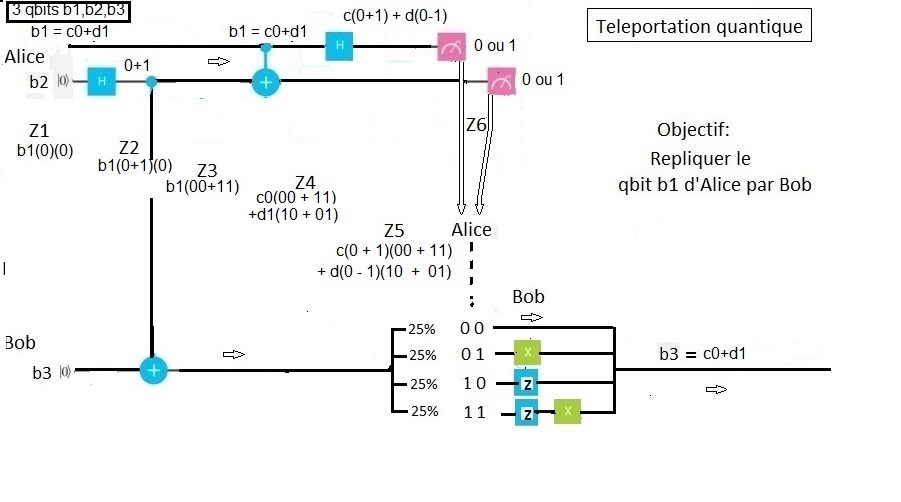
L’evolution des 3 qbits dans le temps s’effectue de gauche à droite.
Les portes quantiques utilisées sont
 H
porte Hadamard qui crée un état superposé en partant d’un état de base
H
porte Hadamard qui crée un état superposé en partant d’un état de base
 C-NOT,
intéressant deux qbits, elle génère leur intrication.
C-NOT,
intéressant deux qbits, elle génère leur intrication.
 Porte
de mesure (mauve) qui projette le qbit sur un bit classique, 0 ou 1
Porte
de mesure (mauve) qui projette le qbit sur un bit classique, 0 ou 1
 Portes
Z et X, qui seront détaillées ci après
Portes
Z et X, qui seront détaillées ci après
Conventions d’écriture : dans toute la suite pour alléger les notations, on ne tiendra pas compte de coefficients numériques comme racine(2) par exemple.
De même, on notera 0 et 1 au lieu des kets |0> et |1> utilisés habituellement.
Exemple : (010) représentera b1=|0>, b2 = |1>, b3 = |0>, l’ordre 1,2,3 étant systématiquement respecté.
Ces zones correspondent à la Source de qbits intriqués schématisée plus haut.
Partant de l’état 0 pour b2 et b3, H crée l’état superposé
(0 + 1) pour b2,
puis avec la porte C-NOT, intrique les qbits en générant l’état
(00) + (11)
b2 b3 ont perdu leur individualité, seul un état commun (00) ou (11) est autorisé
Alice intrique le qbit b1 ( quelconque, à téléporter, sa valeur peut très bien être inconnue d’Alice) avec b2 au moyen d’une porte C-NOT.
A ce stade, les 3 qbits étant intriqués, on conçoit que l’état de b1 puisse être en quelque sorte indirectement intégré avec b3.
Alice applique à b1 une porte Hadamard qui permet de regrouper ( factoriser) les états des qbits b1 et b2
Alice mesure b1 et b0 obtenant une valeur sur 2 bits parmi les 4 possibles et équiprobables : 00, 01, 10 ,11.
Par voie classique (telephone, email...) elle transmet ce resultat à Bob qui applique alors à b3 une transformation adequate pour finaliser la teleportation de b3.
b3 est devenu identique à b1.
 en
Z1
en
Z1
L’état E du système est le produit des 3 qbits
E = b1b2b3 = (c0 + d1)(0)(0)
 en
Z2
en
Z2
b2 est devenu (0 + 1)
E = (c0 + d1)(0 + 1)(0)
 en
Z3
en
Z3
b2 et b3 sont intriqués
E = (c0 + d1)(00 +11)
 en Z4
en Z4
Via la porte
C-NOT, le bit b1 modifie b2 selon la règle :
Si b1 = 0, b2
inchangé, mais si b1 = 1, b2 est inversé
E = c0(00 + 11) +d1(10 + 01)
 en Z5
en Z5
H change b1 = c0 + d1 en b1 = c(0 + 1) + d(0 - 1)
00 °° °°
01 °° °°
10 °° °°
11
°°
°°
E = [ 00(c0 + d1) + 01(c1 + d0) +10(c0 - d1)+ 11(c1 - d0) ]
Alice mesure alors uniquement b1 et b2. Le résultat de chaque mesure est un bit classique, 0 ou 1
Cette mesure partielle préserve l’état résiduel de b3.
En fonction des 2 bits que lui a communiqué Alice, Bob doit maintenant finaliser la teleportation de b3
 00
00
On voit dans l’expression de E ci dessus que l’état résiduel est b3 = (c0 + d1), identique à b1, Bob n’a rien à faire.
 01
01
L’état résiduel est b3 = (c1 + d0).
Pour régénérer b1, Bob doit interchanger les coefficients de 0 et 1.
Ceci s’effectue au moyen d’une porte X.
 10
10
L’état résiduel est b3 = (c0 - d1).
Pour régénérer b1, Bob doit inverser le signe de 1.
Ceci s’effectue au moyen d’une porte Z.
 11
11
L’état résiduel est b3 = (c1 - d0).
Pour régénérer b1, Bob doit à la fois inverser le signe de 1 et interchanger les coefficients de 0 et 1.
Ceci s’effectue en appliquant les portes Z puis X.
 le
qbit original soit détruit
le
qbit original soit détruit
 la
vitesse de l’operation soit inférieure ou égale à celle de la lumière
la
vitesse de l’operation soit inférieure ou égale à celle de la lumière
Une application fascinante est la possibilité de transmettre une direction quelconque de polarisation EXACTEMENT identique.
Par des moyens classiques, on ne pourrait transmettre que des coordonnées sous forme de chiffres, donc forcément limitées en precision...
Quelques rappels sur les notions de base :
Le qubit se compose d’une superposition de deux états de base, par convention nommés |0> et |1> (prononcés : ket 0 et ket 1 ).
Un bit classique se trouve toujours soit dans l’état |0>, soit dans l’état |1> .
Dans le cas général, un qubit se trouve dans une superposition de ces deux états, que l’on peut décrire par une combinaison linéaire des deux états :b = c|0> + d|1> .
Les coefficients c et d sont deux nombres complexes dont la somme des carrée des modules doit être égale à 1.
En se limitant au cas de nombres réel, c et d doivent vérifier c² + d² = 1.
 Porte
H (Hadamard)
Porte
H (Hadamard)
Elle transforme l’ état |0> en un état superposé (|0> + |1>), et l’état |1> en (|0> - |1>)
 Porte
C-NOT
Porte
C-NOT

 Porte
de mesure
Porte
de mesure
Elle projette le qbit vers un bit classique 0 ou 1.
Si b1 = c|0> + d|1>, avec c et d réels, la probabilité de trouver 0 est égale à c², et la probabilité de trouver 1 est égale à d²
 Porte
X
Porte
X
Elle échange les coefficients de |0> et |1>,
(c|0> + d|1>) devient (d|0> + c|1>)
 Porte
Z
Porte
Z
Elle inverse le signe de |1>,
(c|0> + d|1>) devient (c|0> - d|1>)
References
 Qubit
https://fr.wikipedia.org/wiki/Qubit
Qubit
https://fr.wikipedia.org/wiki/Qubit
 "Einstein
aujourd’hui" A.Aspect et Ph. Grangier pp76, CNRS editions, EDP Sciences
"Einstein
aujourd’hui" A.Aspect et Ph. Grangier pp76, CNRS editions, EDP Sciences
 "Quantum
Gates https://en.wikipedia.org/wiki/Quant...
"Quantum
Gates https://en.wikipedia.org/wiki/Quant...
 "Mind,
machines and the multiverse" Julian Brown, Simon & Schuster. Une
presentation très claire du calcul quantique.
"Mind,
machines and the multiverse" Julian Brown, Simon & Schuster. Une
presentation très claire du calcul quantique.
 Site
sympathique pour une entrée en matière
Site
sympathique pour une entrée en matière
https://www.institut-pandore.com/ph...
Enfin IBM donne accès via ce site https://quantum.ibm.com/
à leur processeur et à un simulateur de calcul quantique.
