Qui n’a pas siphonné un jour ou l’autre de l’eau, de l’essence, du vin bien sur !,etc.

Il faut un tuyau assez long pour atteindre la surface du liquide à siphonner d’un coté et de l’autre pour descendre plus bas que cette surface.

Pour amorcer l’opération ce tuyau doit être rempli de liquide par un moyen quelconque, tel que :

— aspiration avec une seringue, à la bouche, avec une poire..

— si l’accès est possible, on noie le tuyau dans le liquide, puis on bouche avec le pouce (ou un bouchon) l’extrémité supérieure que l’on retire prestement du liquide et l’abaisse vers le vase récepteur.

— on met le réservoir fermé sous pression : le liquide passe dans le tuyau

Une fois le siphon amorcé, le liquide coule du niveau le plus haut vers le plus bas et ne s’arrête que lorsque le vase du haut est vide ou que les niveaux se retrouvent à égalité.

On observe que le débit est d’autant plus rapide que la différence des niveaux est importante.

Si la continuité de la veine liquide contenue dans le tuyau est rompue par création d’une bulle (par exemple le tuyau est accidentellement sorti du liquide du vase du haut, même un court instant), le tuyau se vide dans chacun des vases et le siphonnage s’arrête. Il est indispensable de recommencer l’amorçage.

Exemple de siphon classique, dans le laboratoire de l’Université de Nottingham, en Angleterre.

Où est le problème

La grande majorité des explications dans les livres de physique, dictionnaires et encyclopédies fait intervenir la pression atmosphérique dans l’explication du siphon (souvent via l’équation de Bernouilli). Or la vidéo dont sont extraites ces photos démontre sans discussion possible qu’un siphon fonctionne très bien DANS LE VIDE !!

http://www.youtube.com/watch?v=8F4i...

A droite du physicien on voit la boite contenant l’expérience. Cette boite est mise sous un vide poussé. Notons que le liquide utilisé doit résister à l’évaporation sous vide, c’es à dire avoir une tension de vapeur aussi faible que possible. Dans la vidéo il est question de "liquide ionique" ? et un exemple concret serait de l’huile pour pompe à vide par exemple.

Elle comporte deux éprouvettes reliées par un tuyau souple. Avec 3 commandes externes on peut

— faire monter ou descendre le tuyau

— faire monter ou descendre chaque éprouvette

Au démarrage, le tuyau étant situé plus bas que les éprouvettes, il est bien entendu rempli.

Les éprouvettes ont leur liquide au même niveau, principe des vases communicants.

1 On lève le tuyau par sa partie centrale, au dessus du niveau du liquide.

On observe que la veine liquide reste compacte et ne se sépare pas, ce qui prouve que les molécules de ce liquide s’accrochent l’une à l’autre un peu comme de petits aimants

2 On élève l’éprouvette de gauche.

On constate que le liquide coule vers le niveau le plus bas, exactement comme dans le cas d’un siphon normal à la pression atmosphérique !!

Explication proposée

Un siphon fonctionne grâce à la cohésion moléculaire du liquide (par exemple liaisons hydrogène dans le cas de l’eau) et à la GRAVITE.

La pression atmosphérique n’intervient pas dans l’explication du mécanisme d’un siphon.On verra dans le calcul ci dessous qu’elle s’élimine.

A première vue on pourrait comparer la veine de liquide à une CHAÎNE ( Dessin A ci dessous)

et puisque la longueur de chaîne du coté droit est supérieure à celle du coté gauche, avec une chaîne homogène, on voit que la masse supérieure du brin de droite entraîne dans sa chute le brin de gauche.

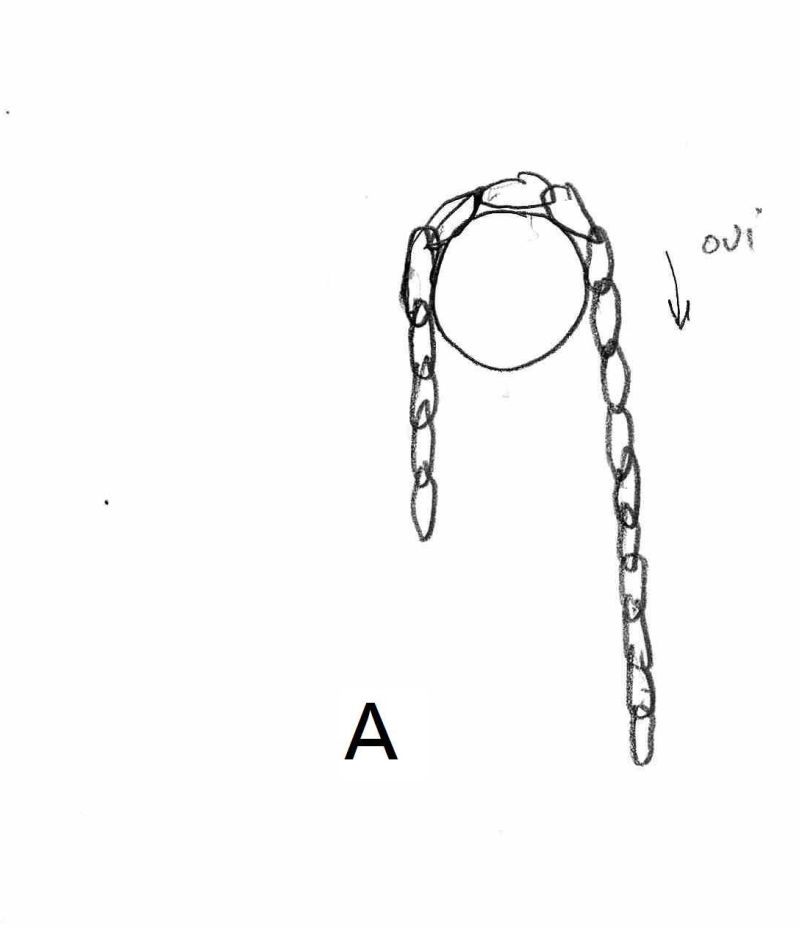
Hélas on ne peut pas comparer une chaîne, objet RIGIDE, à une veine fluide comme le prouvent les figures B et C :

une chaîne à maillons lourds à gauche ne sera pas entraînée par le brin de droite comme dans le cas de la Fig B alors que pour le fluide , le volume (et donc la masse) de liquide pourtant bien supérieur dans le tube à gauche ne posera pas problème et le siphon C fonctionnera normalement.

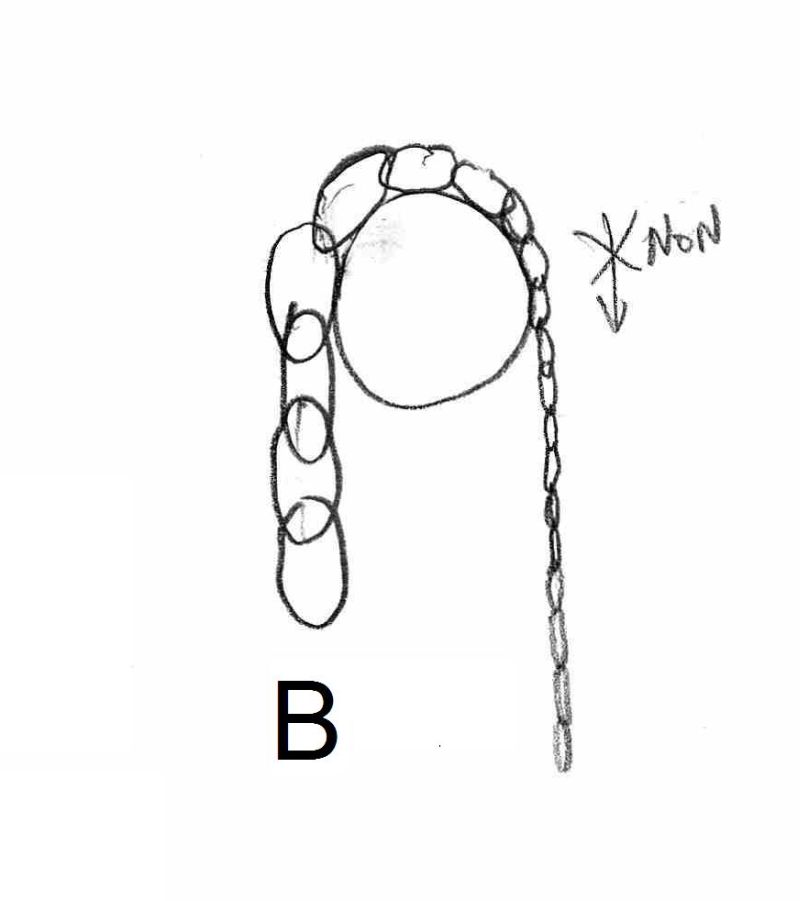
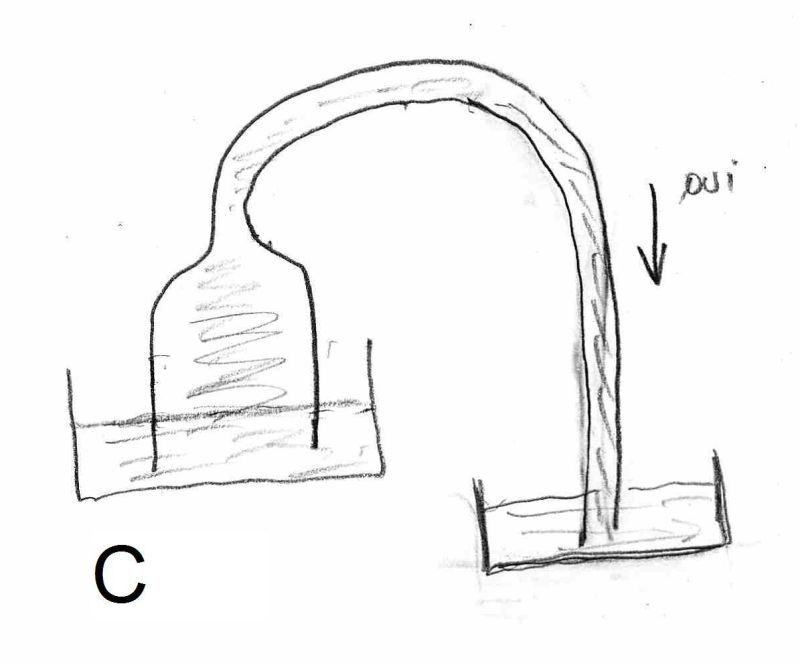
L’explication est que le mouvement du fluide est régi par des différences de PRESSIONS alors que pour les objets rigides, comme les chaines, ce sont les FORCES(poids) qui interviennent.

Plus précisément, en HYDROSTATIQUE on sait que la pression à la base d’une colonne de liquide de hauteur H est égale à H*R*g avec R densité du liquide (masse volumique) et g la gravité.

Exemple : à 10 m sous l’eau, on a 10m*1000kg/m3*9.81m/s² = environ 100 000 Pascals soit 1000hPa

Une même hauteur d’eau dans les branches droite et gauche produit la même pression, indépendamment du diamètre de ces branches .

Calcul d’un siphon

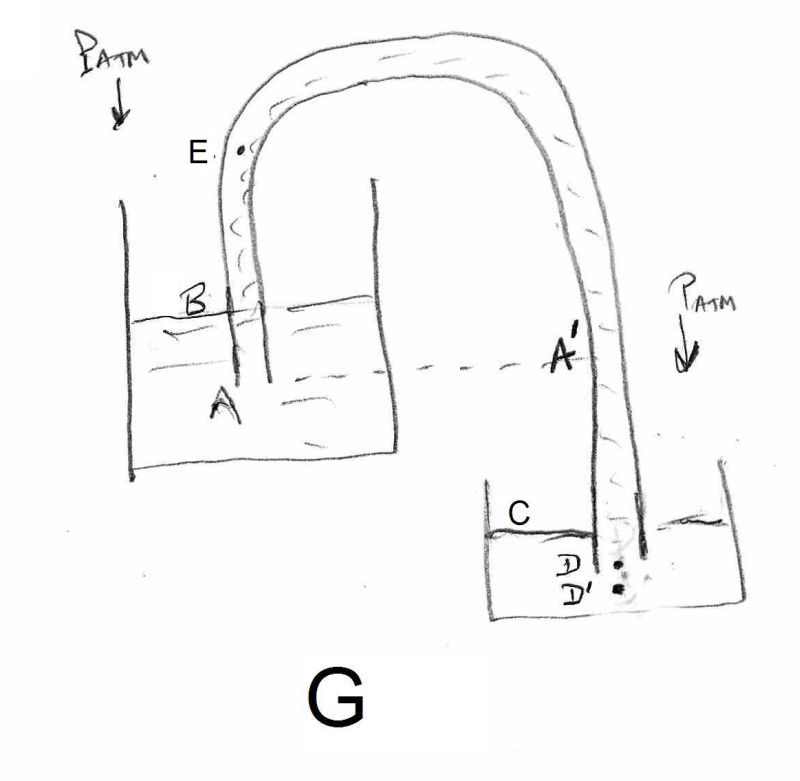
Sur la figure G on va calculer les différentes pressions hydrostatiques (telles qu’on peut les mesurer avec un manomètre du type utilisé sur un tensiomètre, par exemple, et une durit).

L’ensemble est soumis à la pression atmosphérique (C étant plus bas que B, la pression en C est très légèrement supérieure à celle de B d’une valeur totalement négligeable ici).

Le tuyau ACD est parfaitement rempli de liquide. Afin de comprendre le mouvement du liquide, on se place à son extrémité D où la pression est Pd et juste en dessous en D’ où la pression est Pd’ :

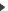  si Pd = Pd’, pas de mouvement de liquide

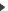  si Pd > Pd’, le liquide descend

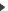  si Pd < Pd’, le liquide monte

Pb = Patmo = Pc

Pa = Pb + AB*R*g

Pd = Pa’ + A’D*R*g Noter que Pa’ = Pa

Pd = Pb + AB*R*g + A’D*R*g

Pd’ = Pc + CD’*R*g

Calculons la différence Pd - Pd’

Pd - Pd’ = Pb + AB*R*g + A’D*R*g - Pc - CD’*R*g

On voit que la pression atmosphérique Patmo = Pb = Pc s’élimine d’elle même, et il reste

Pd - Pd’ = (AB + A’D - CD’)*R*g

Or AB + A’D = BD

Pd - Pd’ = (BD - CD’)*R*g soit quasi BC*R*g

Cette valeur est positive et directement proportionnelle à la différence de hauteur entre les niveaux B et C. Le liquide s’écoule vers le bas de D vers D’.

NOTA : Référence