Déviation de Coriolis
Un tireur situé au pôle nord tire une balle de fusil vers un point C situé sur l’Equateur.
Vue de l’espace ( pour un observateur qui suivrait la Terre dans sa course autour du Soleil mais non sa rotation sur elle même ) , la trajectoire de la balle est une droite : elle avance à une vitesse v, durant un temps t.
Mais pour un observateur terrestre qui se croit immobile, la balle apparaît être déviée vers l’ouest (en réalité on verra que plus généralement, cette déviation est toujours vers la droite ) , d’une distance d.
Il attribue cette déviation à une force, la force de Coriolis.
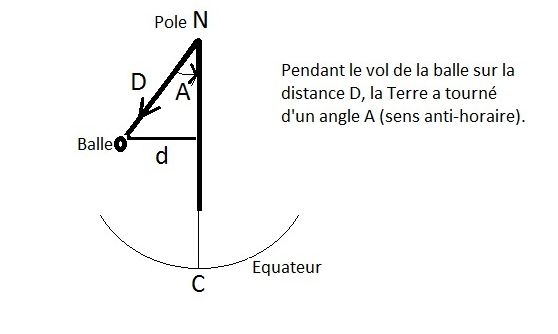
Pendant le temps t, la balle a volé la distance D =v*t, et la Terre a tourné dans le sens anti-horaire, d’un angle A que nous allons calculer.
La Terre tourne à raison de 360° par 24 heures.Il est commode pour le calcul d’exprimer cette vitesse de rotation en radian/seconde ( 1 radian = angle de 57° environ) avec 360° =2Pi * rad.
La vitesse R de rotation de la Terre en radian/seconde est donc
R = 2Pi/(24*3600) = 0.00007 rad/s
Pendant le temps t, la Terre a tourné d’un angle A = R*t
Cet angle est petit, on peut l’assimiler à son sinus ce qui donne
sin(A) = A = d/D soit d = A*D
On remplace A par R*t et obtient
d= R*t*D et comme t=D/v, finalement
d= R*D²/v
La déviation d est donc proportionnelle à la vitesse de rotation de la Terre et au carré de la distance parcourue/vitesse.
Pour une balle de fusil volant à v = 1000 m/s, la déviation d à 100 mètres du tireur, est
d = 0.00007*10 000/1000 = 0.0007m soit 0.7mm
donc négligeable.
Pour un courant marin,ou une masse d’air, circulant à la vitesse de 3 m/s, soit 11 km/h environ, après un parcours de 100km,la déviation est
d=0.00007*(100 000)²/3 = 2.3 km environ
ce qui n’est plus du tout négligeable.
Dans ce cas la vitesse est bien moindre mais la distance parcourue jouant au carré, la déviation par rapport à la ligne droite devient considérable.
Généralisation
Le tireur est maintenant à Paris et veut que sa balle arrive sur le pôle Nord.En prévision de la force de Coriolis qui fera dévier la balle vers la droite de la trajectoire désirée, il oriente la carabine vers sa gauche.
Pour notre observateur situé dans l’espace , la trajectoire de la balle sera une droite qui passe par par le pôle.
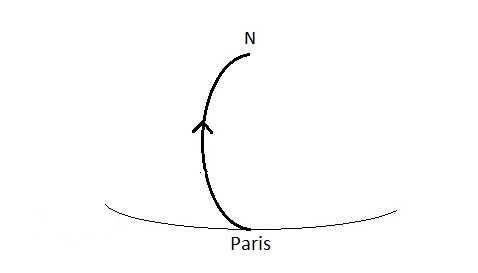
Vue par un observateur fixe sur la Terre, la trajectoire est une courbe, démarrant vers l’ouest et se terminant au pôle nord.
Plus généralement, et ceci n’est pas évident, toute trajectoire ( rectiligne vue de l’Espace) parcourue dans l’hémisphère nord paraîtra courbée vers la droite par rapport au sens du mobile, vue de la Terre.Les sceptiques peuvent se livrer à la petite expérience décrite en Annexe 2.
Dans l’hémisphère nord, la force de Coriolis "tire" toute masse en déplacement vers sa droite, vers sa gauche dans l’hémisphère sud, aucun effet n’étant constaté à l’Équateur.
Interprétation
On voit que cette force n’est en réalité qu’une pseudo force, illusion due au repère en rotation constitué par la Terre.
En effet, vu de l’espace, aucune force ne se manifeste sur la balle qui se déplace en ligne droite, par inertie (notons au passage que celle ci est un Principe), la Terre tournant au dessous de cette trajectoire rectiligne.
Cette force croit avec la latitude du lieu, maximale aux pôles, nulle à l’Équateur.
Conséquences pratiques
Dans l’hémisphère nord, les rivières ont tendance à éroder d’avantage leur rive droite que leur rive gauche.En effet la force de Coriolis "tirant" l’eau vers la berge de droite (par rapport au sens d’écoulement), celle ci subit une usure plus rapide que l’autre berge, à l’origine de la formation des méandres.
Une voie de chemin de fer parcourue par des trains roulant toujours dans le même sens verra son rail droit ( par rapport au sens de circulation du train ) s’user plus que le rail gauche.
Ce phénomène est parfaitement mesurable.
Lors de la Grande Guerre, en 1918 la grosse Bertha, canon ennemi implanté à 110 km de Paris, tirait vers la Capitale des obus de 300 kg avec une vitesse initiale de 1500 m/s.
Après un temps de vol de 3 min environ, la déviation de l’obus à l’arrivée aurait été de près de 1600 m, si elle n’avait été prise en compte par les artilleurs
https://fr.wikipedia.org/wiki/Paris...
Par contre, contrairement à une légende folklorique, le sens de rotation de l’eau dans un lavabo qui se vide est tout à fait aléatoire : la force de Coriolis est négligeable par rapport aux frottements.
Un autre effet concret de la force de Coriolis est observé dans l’experience du pendule de Foucault.
https://fr.wikipedia.org/wiki/Pendu...
En résumé, la pseudo-force de Coriolis cause une déviation apparente des objets mobiles par rapport à la Terre considérée comme fixe.
Dans l’hémisphère nord, cette déviation est orientée vers la droite par rapport au sens de la trajectoire, et ce quelque soit la direction dans laquelle on se dirige :N,S E ou Ouest.
Annexe 1 : calcul de la force de Coriolis
On ré-écrit la déviation en remplaçant D par v*t
d= R*D²/v = R*v²*t²/v = R*v*t²
En dérivant deux fois par rapport au temps, on obtient l’accélération de Coriolis
AccCor = 2R*v
et donc la force de Coriolis sur une masse m au au pôle est :
FCor = 2m*A*v
proportionnelle à la vitesse de rotation terrestre et à la vitesse du mobile.
En un lieu de latitude L (L=0 à l’Equateur et L= 90° au pôle)
FCor = 2m*A*v*sin(L)
Une belle présentation précise et détaillée se trouve sur
http://claude.pastre.free.fr/coriol...
Reprise ici :
Annexe 2 :tracé d’une trajectoire

Sur une feuille de calque, on trace un arc de cercle de rayon 7 cm, centre N et on gradue 7 cm de circonférence tous les cm.
Une épingle en N traverse le calque et en dessous le papier.On aligne les deux repères 7.
En tournant le calque (sens anti-horaire) on amène le 6 du cercle sur la droite.On trace au crayon sur le calque le point à l’aplomb du repère 6 sur la droite.
On continue à tourner le calque en alignant les points du cercle 6,5..1 sur la droite et à tracer les points de trajectoire 6,5..1, puis finalement on relie 1 à N.
La trajectoire est bien courber vers la droite, vue de la Terre, et bien rectiligne vue de l’espace.
Plus généralement, on trace une droite quelconque ne passant pas par N et la gradue de 7 à 1 comme ci dessus.L’épingle toujours en, place, on fait tourner le calque et trace la trajectoire vue de la Terre : on constate qu’elle est systématiquement courbée vers sa droite.

Annexe 3 : calcul en utilisant le Lagrangien
Calcul de la force de Coriolis en utilisant le Lagrangien
On va montrer que l’utilisation de l’énergie d’un système, via son Lagrangien*, permet de limiter les calculs au domaine des scalaires et des dérivées, évitant ainsi la complexité des calculs vectoriels des forces (equation plus classique de Newton).
Un observateur A est fixe, son système d’axes est x,y et un point mobile se déplace à vitesse constante. Les composantes de sa vitesse sont x’(t) et y’(t), dérivées de x et y par rapport au temps t, abréviées x’ et y’ dans la suite.
Un deuxième observateur B est en rotation par rapport à A. Son système d’axes est X,Y.La vitesse angulaire, a, de rotation du repère X,Y est constante.
B perçoit le point mobile se déplaçant à la vitesse X’(t), Y’(t) et ce point lui parait soumis à des forces que nous allons calculer.
Les relations entre les coordonnées x,y et X,Y sont données par :
x = Xcos(a*t) +Ysin(a*t)
y = -X sin(a*t) +Ycos(a*t)
Rappel : Le Lagrangien est la difference entre l’énergie cinétique m*(x’² + y’²)/2 et l’énergie potentielle V(x,y) ( ne ne pas confondre V avec une vitesse).
Le Lagrangien pour A se résume à l’énergie cinétique m*(x’² + y’²)/2, car V=0 le point n’étant soumis à aucune force.
L = m/2(x’² + y’²)
Calculons maintenant ce Lagrangien dans le repère de B.
On commence par dériver x et y par rapport au temps ce qui donne :
x’ = X’cos(a*t) -a*Xsin(a*t) + Y’sin(a*t) + a*Ycos(a*t)
y’ = -X’sin(a*t)- -a*Xcos(a*t) + Y’cos(a*t) -a*Ysin(a*t)
On élève au carré et l’on somme pour obtenir :
x’² + y’² = X’² + Y’² + a²(X² + Y²) +2a( X’Y- Y’X ) (calcul un peu long mais sans difficulté)
D’où l’expression du Lagrangien dans le système en rotation
L = m/2(x’² + y’²) = m/2(X’² + Y’²) + m/2*a²(X² + Y²) +m*a( X’Y- Y’X )
Le premier terme
m/2(X’² + Y’²)
est l’énergie cinétique.
Pour interpreter le deuxième terme du Lagrangien, on pose
V = m/2*a²(X² + Y²)
Ce potentiel correspond à une force F= -dV/dr, soit
F selon X = -dV/dX = -m*a²X
F selon Y = -dV/dY = -m*a²Y
C’est la force centrifuge, proportionnelle au carré de la vitesse de rotation et à la distance de l’origine, négative car elle éloigne l’objet du repère mobile.
Il reste à expliciter le 3ème terme du Lagrangien.
Pour cela on utilise l’equation d’Euler-Lagrange pour X et Y
d/dt(dL/dX’) = dL/dX
d/dt(dL/dY’) = dL/dY
avec
L = m/2(X’² + Y’²) + m/2*a²(X² + Y²) +m*a( X’Y- Y’X )
Commençons par X’ et X
dL/dX’ = m* X’ + m*aY d’où d/dt(dL/dX’) = m*X"+ m*aY’
dL/dX = m*a²X -m*aY’
et en égalant
m*X"+ m*aY’= m*a²X -m*aY’
soit
m*X" = m*a²X -2m*aY’
Le même calcul pour Y donne
m*Y" = m*a²Y + 2m*aX’
La force totale (m*X",m*Y") est donc la somme de la force centrifuge (m/2X’², m/2Y’²) , et de la force de Coriolis (-2m*aY’,+ 2m*aX’) dont les composantes sont proportionnelles à la vitesse (X’ et Y’).
On note que cette force de Coriolis est proportionnelle à la vitesse du mobile, à la vitesse de rotation du repère tournant et orthogonale à la trajectoire.
En effet, le produit scalaire du vecteur vitesse par la force de Coriolis est toujours nul
(Vecteur vitesse) * Fcor = X’*(-2m*aY’) + Y’*(2m*aX’) = 0
*Reference : "Classical Mechanics, The Theoretical Minimum "par Leonard Susskind, un excellent livre de vulgarisation à bon niveau.Aussi recommandable, par le même auteur : "Quantum mechanics, The Theoretical Minimum".
Remerciements
A Alain (cosmic92), danielcrb et Pierre V. pour leur aide dans la rectification de mes erreurs de...trajectoire...
